DC/AC converters (inverters)

DC to AC converters produce an AC output waveform from a DC source. Applications include adjustable speed drives (ASD), uninterruptible power supplies (UPS), Flexible AC transmission systems (FACTS), voltage compensators, and photovoltaic inverters. Topologies for these converters can be separated into two distinct categories: voltage source inverters and current source inverters. Voltage source inverters (VSIs) are named so because the independently controlled output is a voltage waveform. Similarly, current source inverters (CSIs) are distinct in that the controlled AC output is a current waveform.

DC to AC power conversion is the result of power switching devices, which are commonly fully controllable semiconductor power switches. The output waveforms are therefore made up of discrete values, producing fast transitions rather than smooth ones. For some applications, even a rough approximation of the sinusoidal waveform of AC power is adequate. Where a near sinusoidal waveform is required, the switching devices are operated much faster than the desired output frequency, and the time they spend in either state is controlled so the averaged output is nearly sinusoidal. Common modulation techniques include the carrier-based technique, or Pulse-width modulation, space-vector technique, and the selective-harmonic technique.^[4]

Voltage source inverters have practical uses in both single-phase and three-phase applications. Single-phase VSIs utilize half-bridge and full-bridge configurations, and are widely used for power supplies, single-phase UPSs, and elaborate high-power topologies when used in multicell configurations. Three-phase VSIs are used in applications that require sinusoidal voltage waveforms, such as ASDs, UPSs, and some types of FACTS devices such as the STATCOM. They are also used in applications where arbitrary voltages are required as in the case of active power filters and voltage compensators.^[4]

Current source inverters are used to produce an AC output current from a DC current supply. This type of inverter is practical for three-phase applications in which high-quality voltage waveforms are required.

A relatively new class of inverters, called multilevel inverters, has gained widespread interest. Normal operation of CSIs and VSIs can be classified as two-level inverters, due to the fact that power switches connect to either the positive or to the negative DC bus. If more than two voltage levels were available to the inverter output terminals, the AC output could better approximate a sine wave. It is for this reason that multilevel inverters, although more complex and costly, offer higher performance.^[5]

Each inverter type differs in the DC links used, and in whether or not they require freewheeling diodes. Either can be made to operate in square-wave or pulse-width modulation (PWM) mode, depending on its intended usage. Square-wave mode offers simplicity, while PWM can be implemented several different ways and produces higher quality waveforms.^[4]

Voltage Source Inverters (VSI) feed the output inverter section from an approximately constant-voltage source.^[4]

The desired quality of the current output waveform determines which modulation technique needs to be selected for a given application. The output of a VSI is composed of discrete values. In order to obtain a smooth current waveform, the loads need to be inductive at the select harmonic frequencies. Without some sort of inductive filtering between the source and load, a capacitive load will cause the load to receive a choppy current waveform, with large and frequent current spikes.^[4]

There are three main types of VSIs:

1. Single-phase half-bridge inverter
2. Single-phase full-bridge inverter
3. Three-phase voltage source inverter

Single-phase half-bridge inverter[edit]

Figure 8: The AC input for an ASD.

FIGURE 9: Single-Phase Half-Bridge Voltage Source Inverter

The single-phase voltage source half-bridge inverters, are meant for lower voltage applications and are commonly used in power supplies.^[4] Figure 9 shows the circuit schematic of this inverter.

Low-order current harmonics get injected back to the source voltage by the operation of the inverter. This means that two large capacitors are needed for filtering purposes in this design.^[4] As Figure 9 illustrates, only one switch can be on at time in each leg of the inverter. If both switches in a leg were on at the same time, the DC source will be shorted out.

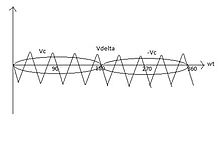
Inverters can use several modulation techniques to control their switching schemes. The carrier-based PWM technique compares the AC output waveform, v_c, to a carrier voltage signal, v_Δ. When v_c is greater than v_Δ, S+ is on, and when v_c is less than v_Δ, S- is on. When the AC output is at frequency fc with its amplitude at v_c, and the triangular carrier signal is at frequency f_Δ with its amplitude at v_Δ, the PWM becomes a special sinusoidal case of the carrier based PWM.^[4] This case is dubbed sinusoidal pulse-width modulation (SPWM).For this, the modulation index, or amplitude-modulation ratio, is defined as m_a = v_c/v_∆ .

The normalized carrier frequency, or frequency-modulation ratio, is calculated using the equation m_f = f_∆/f_c .

If the over-modulation region, ma, exceeds one, a higher fundamental AC output voltage will be observed, but at the cost of saturation. For SPWM, the harmonics of the output waveform are at well-defined frequencies and amplitudes. This simplifies the design of the filtering components needed for the low-order current harmonic injection from the operation of the inverter. The maximum output amplitude in this mode of operation is half of the source voltage. If the maximum output amplitude, m_a, exceeds 3.24, the output waveform of the inverter becomes a square wave.^[4]

As was true for PWM, both switches in a leg for square wave modulation cannot be turned on at the same time, as this would cause a short across the voltage source. The switching scheme requires that both S+ and S- be on for a half cycle of the AC output period.^[4] The fundamental AC output amplitude is equal to v_o1 = v_aN = 2v_i/π .

Its harmonics have an amplitude of v_oh = v_o1/h.

Therefore, the AC output voltage is not controlled by the inverter, but rather by the magnitude of the DC input voltage of the inverter.^[4]

Using selective harmonic elimination (SHE) as a modulation technique allows the switching of the inverter to selectively eliminate intrinsic harmonics. The fundamental component of the AC output voltage can also be adjusted within a desirable range. Since the AC output voltage obtained from this modulation technique has odd half and odd quarter wave symmetry, even harmonics do not exist.^[4] Any undesirable odd (N-1) intrinsic harmonics from the output waveform can be eliminated.

Single-phase full-bridge inverter[edit]

FIGURE 3: Single-Phase Voltage Source Full-Bridge Inverter

FIGURE 4: Carrier and Modulating Signals for the Bipolar Pulsewidth Modulation Technique

The full-bridge inverter is similar to the half bridge-inverter, but it has an additional leg to connect the neutral point to the load.^[4]Figure 3 shows the circuit schematic of the single-phase voltage source full-bridge inverter.

To avoid shorting out the voltage source, S1+ and S1- cannot be on at the same time, and S2+ and S2- also cannot be on at the same time. Any modulating technique used for the full-bridge configuration should have either the top or the bottom switch of each leg on at any given time. Due to the extra leg, the maximum amplitude of the output waveform is Vi, and is twice as large as the maximum achievable output amplitude for the half-bridge configuration.^[4]

States 1 and 2 from Table 2 are used to generate the AC output voltage with bipolar SPWM. The AC output voltage can take on only two values, either Vi or –Vi. To generate these same states using a half-bridge configuration, a carrier based technique can be used. S+ being on for the half-bridge corresponds to S1+ and S2- being on for the full-bridge. Similarly, S- being on for the half-bridge corresponds to S1- and S2+ being on for the full bridge. The output voltage for this modulation technique is more or less sinusoidal, with a fundamental component that has an amplitude in the linear region of less than or equal to one^[4]v_o1 =v_ab1= v_i • m_a.

Unlike the bipolar PWM technique, the unipolar approach uses states 1, 2, 3 and 4 from Table 2 to generate its AC output voltage. Therefore, the AC output voltage can take on the values Vi, 0 or –V [1]i. To generate these states, two sinusoidal modulating signals, Vc and –Vc, are needed, as seen in Figure 4.

Vc is used to generate VaN, while –Vc is used to generate VbN. The following relationship is called unipolar carrier-based SPWM v_o1 =2 • v_aN1= v_i • m_a.

The phase voltages VaN and VbN are identical, but 180 degrees out of phase with each other. The output voltage is equal to the difference of the two phase voltages, and do not contain any even harmonics. Therefore, if mf is taken, even the AC output voltage harmonics will appear at normalized odd frequencies, fh. These frequencies are centered on double the value of the normalized carrier frequency. This particular feature allows for smaller filtering components when trying to obtain a higher quality output waveform.^[4]

As was the case for the half-bridge SHE, the AC output voltage contains no even harmonics due to its odd half and odd quarter wave symmetry.^[4]

Three-phase voltage source inverter[edit]

FIGURE 5: Three-Phase Voltage Source Inverter Circuit Schematic

FIGURE 6: Three-Phase Square-Wave Operation a) Switch State S1 b) Switch State S3 c) S1 Output d) S3 Output

Single-phase VSIs are used primarily for low power range applications, while three-phase VSIs cover both medium and high power range applications.^[4] Figure 5 shows the circuit schematic for a three-phase VSI.

Switches in any of the three legs of the inverter cannot be switched off simultaneously due to this resulting in the voltages being dependent on the respective line current's polarity. States 7 and 8 produce zero AC line voltages, which result in AC line currents freewheeling through either the upper or the lower components. However, the line voltages for states 1 through 6 produce an AC line voltage consisting of the discrete values of Vi, 0 or –Vi.^[4]

For three-phase SPWM, three modulating signals that are 120 degrees out of phase with one another are used in order to produce out of phase load voltages. In order to preserve the PWM features with a single carrier signal, the normalized carrier frequency, mf, needs to be a multiple of three. This keeps the magnitude of the phase voltages identical, but out of phase with each other by 120 degrees.^[4] The maximum achievable phase voltage amplitude in the linear region, ma less than or equal to one, is v_phase = v_i / 2. The maximum achievable line voltage amplitude is V_ab1 = v_ab • √3 / 2

The only way to control the load voltage is by changing the input DC voltage.

Current source inverters[edit]

FIGURE 7: Three-Phase Current Source Inverter

Figure 8: Synchronized-Pulse-Width-Modulation Waveforms for a Three-Phase Current Source Inverter a) Carrier and Modulating Signals b) S1 State c) S3 State d) Output Current

Figure 9: Space-Vector Representation in Current Source Inverters

Current source inverters convert DC current into an AC current waveform. In applications requiring sinusoidal AC waveforms, magnitude, frequency, and phase should all be controlled. CSIs have high changes in current over time, so capacitors are commonly employed on the AC side, while inductors are commonly employed on the DC side.^[4] Due to the absence of freewheeling diodes, the power circuit is reduced in size and weight, and tends to be more reliable than VSIs.^[5] Although single-phase topologies are possible, three-phase CSIs are more practical.

In its most generalized form, a three-phase CSI employs the same conduction sequence as a six-pulse rectifier. At any time, only one common-cathode switch and one common-anode switch are on.^[5]

As a result, line currents take discrete values of –ii, 0 and ii. States are chosen such that a desired waveform is output and only valid states are used. This selection is based on modulating techniques, which include carrier-based PWM, selective harmonic elimination, and space-vector techniques.^[4]

Carrier-based techniques used for VSIs can also be implemented for CSIs, resulting in CSI line currents that behave in the same way as VSI line voltages. The digital circuit utilized for modulating signals contains a switching pulse generator, a shorting pulse generator, a shorting pulse distributor, and a switching and shorting pulse combiner. A gating signal is produced based on a carrier current and three modulating signals.^[4]

A shorting pulse is added to this signal when no top switches and no bottom switches are gated, causing the RMS currents to be equal in all legs. The same methods are utilized for each phase, however, switching variables are 120 degrees out of phase relative to one another, and the current pulses are shifted by a half-cycle with respect to output currents. If a triangular carrier is used with sinusoidal modulating signals, the CSI is said to be utilizing synchronized-pulse-width-modulation (SPWM). If full over-modulation is used in conjunction with SPWM the inverter is said to be in square-wave operation.^[4]

The second CSI modulation category, SHE is also similar to its VSI counterpart. Utilizing the gating signals developed for a VSI and a set of synchronizing sinusoidal current signals, results in symmetrically distributed shorting pulses and, therefore, symmetrical gating patterns. This allows any arbitrary number of harmonics to be eliminated.^[4] It also allows control of the fundamental line current through the proper selection of primary switching angles. Optimal switching patterns must have quarter-wave and half-wave symmetry, as well as symmetry about 30 degrees and 150 degrees. Switching patterns are never allowed between 60 degrees and 120 degrees. The current ripple can be further reduced with the use of larger output capacitors, or by increasing the number of switching pulses.^[5]

The third category, space-vector-based modulation, generates PWM load line currents that equal load line currents, on average. Valid switching states and time selections are made digitally based on space vector transformation. Modulating signals are represented as a complex vector using a transformation equation. For balanced three-phase sinusoidal signals, this vector becomes a fixed module, which rotates at a frequency, ω. These space vectors are then used to approximate the modulating signal. If the signal is between arbitrary vectors, the vectors are combined with the zero vectors I7, I8, or I9.^[4] The following equations are used to ensure that the generated currents and the current vectors are on average equivalent.

Multilevel inverters[edit]

FIGURE 10: Three-Level Neutral-Clamped Inverter

A relatively new class called multilevel inverters has gained widespread interest. Normal operation of CSIs and VSIs can be classified as two-level inverters because the power switches connect to either the positive or the negative DC bus.^[5] If more than two voltage levels were available to the inverter output terminals, the AC output could better approximate a sine wave.^[4] For this reason multilevel inverters, although more complex and costly, offer higher performance.^[5] A three-level neutral-clamped inverter is shown in Figure 10.

Control methods for a three-level inverter only allow two switches of the four switches in each leg to simultaneously change conduction states. This allows smooth commutation and avoids shoot through by only selecting valid states.^[5] It may also be noted that since the DC bus voltage is shared by at least two power valves, their voltage ratings can be less than a two-level counterpart.

Carrier-based and space-vector modulation techniques are used for multilevel topologies. The methods for these techniques follow those of classic inverters, but with added complexity. Space-vector modulation offers a greater number of fixed voltage vectors to be used in approximating the modulation signal, and therefore allows more effective space vector PWM strategies to be accomplished at the cost of more elaborate algorithms. Due to added complexity and number of semiconductor devices, multilevel inverters are currently more suitable for high-power high-voltage applications.^[5] This technology reduces the harmonics hence improves overall efficiency of the scheme.